Jika persamaan yang diberikan berbentuk 
, maka variabel y yang muncul di ruas kanan mengakibatkan tidak bisa dipecahkan dengan cara integrasi langsung. Dengan demikian, untuk memecahkan persamaan differensial yang berbentuk digunakan cara memisahkan variabel-variabel penyusunnya sebelum melakukan peng-integral-an. Perhatikan kedua bentuk umum persamaan di bawah ini :
- Perkalian
Jika persamaan yang diberikan berbentuk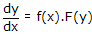
, maka dengan memisahkan variabel-variabelnya diperoleh persamaan 
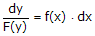. Setelah persamaan yang baru ini terbentuk, kita dapat menggunakan integrasi langsung untuk menyelesaikannya, sehingga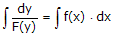 
Contoh :
Pecahkan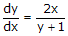
Solusi : (y + 1) dy = 2x dx
Jika kedua ruas di-integrasikan, maka : ∫(y + 1) dy = ∫2x dx
Jadi :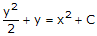
- Pembagian
Jika persamaan yang diberikan berbentuk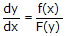
, maka dengan memisahkan variabel-variabelnya diperoleh persamaan 
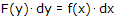. Setelah persamaan yang baru ini terbentuk, kita dapat menggunakan integrasi langsung untuk menyelesaikannya, sehingga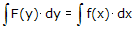 
Contoh :
Pecahkan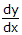
= (1 + x)(1 + y)
Solusi :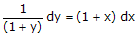
Jika kedua ruas di-integrasikan, maka :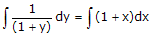
Jadi :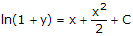
0 comments:
Post a Comment