Bentuk :
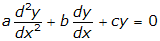
Persamaan karakteristik diperoleh :
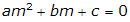
dimana 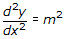 ;
;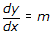 dan y= 1
dan y= 1
Pemecahan persamaan diferensial orde kedua tergantung pada akar-akar persamaan karakteristiknya. Apabila :
- Kedua akarnya riil dan berbeda, dimana m = m1 dan m = m2
Maka solusinya :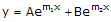
Contoh : Pecahkan persamaan differensial orde kedua berikut
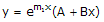
Pada persamaan differensial di atas, persamaan karakteristiknya menjadi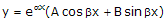 . Sehingga akar-akarnya berbentuk
. Sehingga akar-akarnya berbentuk 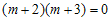 dimana
dimana 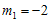 dan
dan 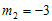 . Dengan demikian solusi untuk persamaan
. Dengan demikian solusi untuk persamaan 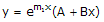 adalah
adalah 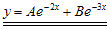
Pembuktian :
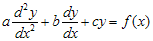
Jika f(x) = 0, maka persamaannya :
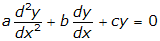
Misalkan y = u dan y = v (u dan v fungsi dari x), sehingga berdasarkan persamaan di atas diperoleh
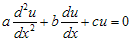 dan
dan 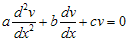
Dengan menggabungkan keduanya, maka
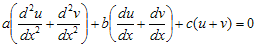
Dari persamaan di atas, diketahui bahwa
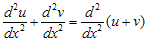 dan
dan 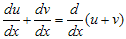
Sehingga persamaan di atas juga dapat ditulis
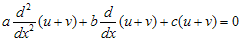
Pada persamaan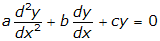 , jika a = 0, maka diperoleh persamaan orde pertama
, jika a = 0, maka diperoleh persamaan orde pertama 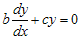 , yaitu
, yaitu 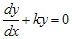 dengan
dengan 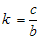
Dengan pemisahan variabel :
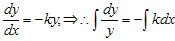
Jadi :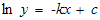
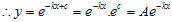 (karena ec konstan)
(karena ec konstan)
Jika -k dinyatakan dengan m, maka persamaan di atas dapat ditulis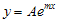 . Dengan melakukan substitusi ke bentuk persamaan differensial orde kedua dimana
. Dengan melakukan substitusi ke bentuk persamaan differensial orde kedua dimana 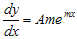 dan
dan 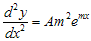 , diperoleh
, diperoleh 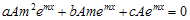 . Jika kedua ruas dibagi dengan
. Jika kedua ruas dibagi dengan 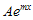 , maka
, maka 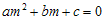 . Bentuk persamaan kuadrat ini memberikan dua akar m = m1 dan m = m2, sehingga diperoleh dua pemecahan bagi persamaan semmula yaitu
. Bentuk persamaan kuadrat ini memberikan dua akar m = m1 dan m = m2, sehingga diperoleh dua pemecahan bagi persamaan semmula yaitu 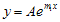 dan
dan 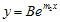 . Dengan demikian, pemecahan untuk persamaan differensial orde kedua yang berbentuk
. Dengan demikian, pemecahan untuk persamaan differensial orde kedua yang berbentuk 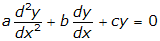 adalah
adalah 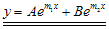
- Kedua akarnya riil dan sama, dimana m = m1 atau m = m2
Maka solusinya :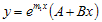
Contoh : Pecahkan persamaan differensial orde kedua berikut
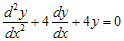
Pada persamaan differensial di atas, persamaan karakteristiknya menjadi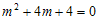 . Sehingga akar-akarnya berbentuk
. Sehingga akar-akarnya berbentuk 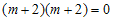 dimana
dimana 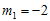 (dua kali). Dengan demikian solusi untuk persamaan
(dua kali). Dengan demikian solusi untuk persamaan 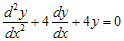 adalah
adalah 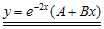
Pembuktian :
Jika akar - akarnya m = m1 = m2, maka pemecahan persamaan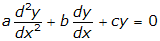 adalah
adalah 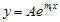 dan
dan 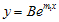 . Akan tetapi, karena setiap persamaan differensial orde kedua selalu memberikan dua buah konstanta sembarang, maka harus ada suku lain yang memuat konstanta kedua tersebut, yaitu
. Akan tetapi, karena setiap persamaan differensial orde kedua selalu memberikan dua buah konstanta sembarang, maka harus ada suku lain yang memuat konstanta kedua tersebut, yaitu 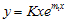 . Sehingga pemecahan untuk persamaan
. Sehingga pemecahan untuk persamaan 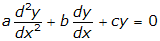 akan menjadi
akan menjadi 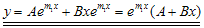
- Kedua akarnya kompleks, dimana m = α ± jβ
Maka solusinya :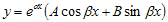
Contoh : Pecahkan persamaan differensial orde kedua berikut
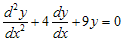
Pada persamaan differensial di atas, persamaan karakteristiknya menjadi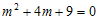 . Sehingga nilai akar-akarnya :
. Sehingga nilai akar-akarnya :
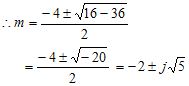
Dari akar-akar di atas diketahui bahwa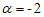 dan
dan 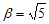 . Dengan demikian solusi untuk persamaan
. Dengan demikian solusi untuk persamaan 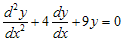 adalah
adalah 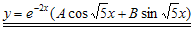
Pembuktian :
Jika akar - akarnya kompleks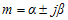 , yaitu
, yaitu 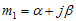 dan
dan 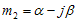 , maka pemecahan persamaan
, maka pemecahan persamaan 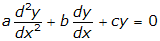 adalah :
adalah :
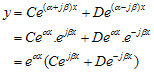
Ingat bahwa:
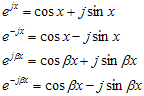
Maka :
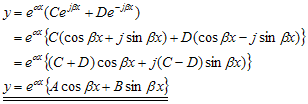
dengan:
A = (C+D)
B = j(C-D)
Untuk persamaan yang memiliki bentuk 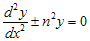 , perhatikan persamaan
, perhatikan persamaan 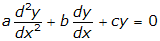 . Jika b = 0, maka :
. Jika b = 0, maka :
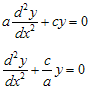
Bentuk persamaan di atas dapat ditulis sebagai 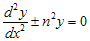 , yang mencakup kedua kemungkinan koefisien y (positif atau negatif). Solusi untuk persamaan ini adalah :
, yang mencakup kedua kemungkinan koefisien y (positif atau negatif). Solusi untuk persamaan ini adalah :
- Jika
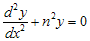 , maka
, maka 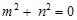
Berdasarkan persamaan di atas, maka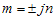 . Bentuk ini serupa dengan
. Bentuk ini serupa dengan 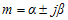 dimana α = 0 dan β = n. Dengan demikian solusi untuk persamaan yang memiliki bentuk
dimana α = 0 dan β = n. Dengan demikian solusi untuk persamaan yang memiliki bentuk 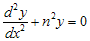 adalah
adalah 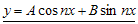
Contoh : Pecahkan persamaan differensial orde kedua berikut
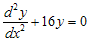
Pada persamaan di atas diketahui bahwa n = 16, sehingga
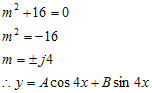
- Jika
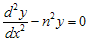 , maka
, maka 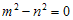
Berdasarkan persamaan di atas, maka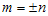 , sehingga
, sehingga 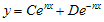 . Ingat bahwa :
. Ingat bahwa :
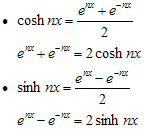
Jika kedua persamaan tersebut dijumlahkan, maka diperoleh

Jika kedua persamaan tersebut dikurangkan, maka diperoleh
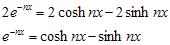
Dengan demikian,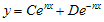 dapat ditulis sebagai
dapat ditulis sebagai
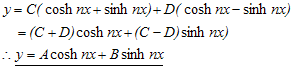
Contoh : Pecahkan persamaan differensial orde kedua berikut
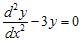
Pada persamaan di atas diketahui bahwa n = 3, sehingga
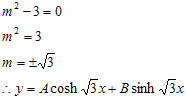
Pemecahan Lengkap Persamaan Differensial Orde Kedua
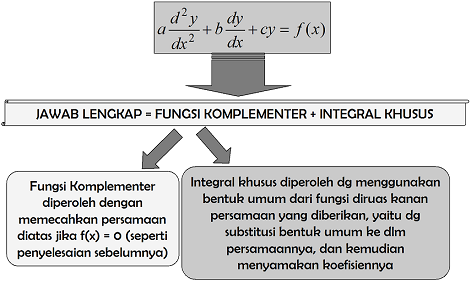
Di bawah ini tabel bentuk umum integral khusus.
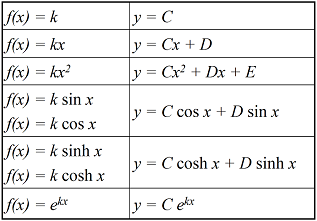
Contoh :
Pecahkan persamaan differensial 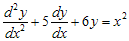
- Fungsi Komplementer (FK)
Fungsi Komplementer (FK) diperoleh jika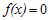 . Sehingga persamaan karakteristiknya adalah :
. Sehingga persamaan karakteristiknya adalah :
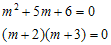
Dari persamaan di atas diketahui bahwa m1 = -2 dan m2 = -3. Dengan demikian fungsi komplementernya adalah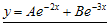
- Integral Khusus (IK)
Perhatikan persamaan pada ruas kanan dan sesuaikan dengan tabel di atas. Karena ruas kanan berbentuk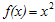 , maka berdasarkan tabel di atas untuk integral khusus digunakan bentuk umum berderajat dua. Jadi, bentuk umum ruas kanan menjadi
, maka berdasarkan tabel di atas untuk integral khusus digunakan bentuk umum berderajat dua. Jadi, bentuk umum ruas kanan menjadi
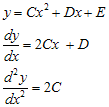
Dengan melakukan substitusi persamaan-persamaan di atas ke dalam persamaan sebenarnya, diperoleh
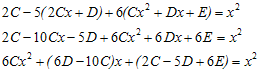
Selanjutnya, samakan koefisien-koefisien x yang memiliki pangkat sama antara ruas kiri dan ruas kanan
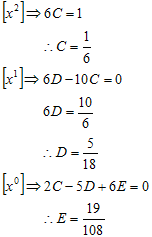
Jadi integral khusus-nya adalah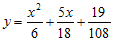
Jawaban sebenarnya untuk persamaan 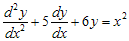 adalah penjumlahan dari Fungsi Komplementer (FK) dan Integral Khusus (IK). Jadi penyelesaian untuk
adalah penjumlahan dari Fungsi Komplementer (FK) dan Integral Khusus (IK). Jadi penyelesaian untuk 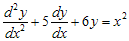 adalah
adalah 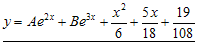


3 comments:
Keren b=gan, bermanfaat sekali. Semoga semakin banyak sharing dan kebaikan kembali ke diri agan sendiri
Gan izin brtanya.m1 sma m2 nya ad ktentuan ga? Msalnya m1>m2 atau m2>m1?
Goodjob
Post a Comment