Pemecahan Persamaan Diferensial (Cara 1)

Pada cara pertama ini, pemecahan persamaan differential dilakukan dengan cara integrasi langsung. Artinya, jika persamaan yang diberikan dapat disusun dalam bentuk = f(x), maka persamaan tersebut dapat dipecahkan dengan integrasi sederhana.

Contoh :

1. Tentukan y jika 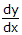= 3x² – 6x + 5
   Maka, y = ∫(3x² – 6x + 5)dx = x³ – 3x² + 5x + C
   Jadi y = x³ – 3x² + 5x + C
   Keterangan : harga C tidak dapat ditentukan, kecuali diberi keterangan tambahan tentang fungsi tersebut.
2. Pecahkan x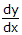= 5x³ + 4
   =
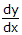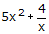
   Sehingga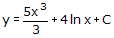
3. Pecahkan e^x 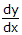= 4, jika diberikan bahwa y = 3 untuk x = 0
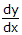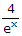   = = 4e^-x
   Sehingga y = ∫4e^-x dx = -4e^-x + C
   Jika diberikan y = 3 untuk x = 0, maka 3 = -4e⁰ + C dan nilai C = 7
   Sehingga y = -4e^-x + 7

Please Give Us Your 1 Minute In Sharing This Post!

SOCIALIZE IT →

Tweet

FOLLOW US →

SHARE IT →

Powered By: BloggerYard.Com